Diccionario de Finanzas y Derecho: La curva de Laffer

  Miguel Ángel Bernal es profesor del IEB¿Se puede recaudar más bajando impuestos?  A esta pregunta que ha estado en la cabeza de los economistas durante mucho tiempose enfrentó Arthur Laffer en la década de los 80.  Su respuesta fue un gráfico con forma de U invertida, ver  gráfico.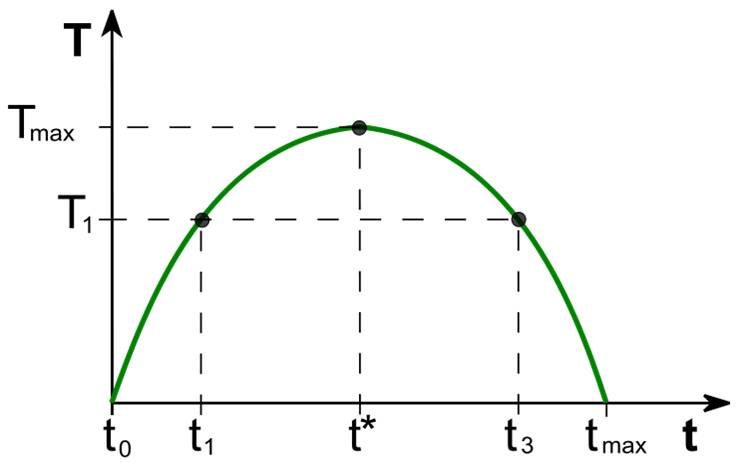Partiendo de los tipos impositivos (abscisas, t) como variable independiente, gráfico los ingresos fiscales totales (ordenadas, T).  Razona que en caso de que el tipo impositiva fuera del 0% (t₀)  no se recaudaría nada, lo cual también ocurriría si el tipo impositivo fuese del 100% (t_max) pues nadie está dispuesta a entregar la totalidad de sus renta al estado.    La curva tendría un punto máximo (t^*) que es el tipo impositivo que maximiza la recaudación fiscal (T_max), consiguiendo el Estado por tanto la eficiencia fiscal.  Partiendo de esta cantidad máxima, la curva pone de manifiesto que se puede obtener una recaudación inferior (T₁) a través de dos tipos impositivos diferentes:  t₁ y t_2, además de cómo se ha comentado existe una recaudación máxima.  En base a esta afirmación se puede enunciar que los tipos fiscales más eficientes se situarían entre 0%(t₀) y t^*, siendo ineficientes o penalizadores para los ciudadanos tipos impositivos mayores a t^*.El teorema de Rolle desvela la validez matemática del postulado de Laffer,  la clave por tanto está en determinar la tasa eficiente (t^*).  En este sentido el trabajo de Mathias Trabandt y Harald Uhling, quizá el punto de referencia actual, establecen un valor alrededor del 70% de tipo impositivo eficiente; asimismo redibujan la curva de una forma asimétrica tal y como se puede ver en el gráfico 2.El debate sobre el postulado de Laffer y los posteriores estudios y modificaciones es de plena actualidad en el contexto recesivo y de restricciones públicas